In the modern world of image processing, nobody thinks about about “simple” tasks such as the rotation, shearing or mirroring of an image because such functions have become so standardized, that even the simplest photoviewers include them. Nevertheless, besides their abundance, a lot of programmers do not know the underlying algorithms. Whilst it is easy to understand the short transformation algorithms for shearing or mirroring (which only include a few calculations and/or assignment of values), algorithms for rotation of matrices (such as images) through an arbitrary angle are more complex in comparison.

One of my favourite algorithms in the one presented by Alan W. Paeth in the year 1986 (Graphics Interface). In this paper, Paeth describes a rotation algorithm which uses 3 consecutive shear operations to perform arbitrary angle rotation. In contrast to many other rotation algorithms, Paeths method produces exact values for for rotations with multiples of 90°

Needed values

Peath defines 2 values needed to perform the shearing operations:

• α (alpha): Angle for X-Axis rotations
• β (beta): Angle for Y-Axis rotations

These two angles will be calculated from the given rotation angle θ (theta; in radians) with following formulas:

• α = -tan(θ/2)
• β = sin(θ)

These angles will then be used to perform the following 3 shear operations:

1. x = x + α * y
2. y = y + β * x
3. x = x + α * y

If applied to each point of the image, these two shears will rotate the image through 45° (around the point 0|0). Due to the fact that the usual coordinate system in programming is upside down, the rotation is counterclockwise.

Example

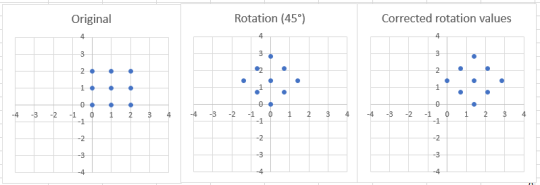
Imagine you would like to rotate an image or matrix through 45°. At first, you had to calculate α and β for the shear operations. To do so, you have to keep in mind that the algorithm uses the angle given in radians, so you have to first transform the given angle from degree to radians. This is easy done:

• θ_radians = θ * 0,0174533 = 45° * 0,0174533 = 0,7853985 rad

If you have the angle given in radians, you are able to calculate the respective shear angles:

• α = -tan(θ/2) = -tan(0,7853985/2) = -0,41 rad
• β = sin(θ) = sin(0,7853985) = 0,71 rad

These values are fixed throughout the rest of the algorithm, so the calculation has to be performed only once. After the calculation of the shearing angles, each point of the image has to be sheared. I will calculate the sheared points exemplary for 4 different points:

1. P(0;0):
   • First shear: x = 0 + (-0,41) * 0 = 0
   • Second shear: y = 0 + 0.71 * 0 = 0
   • Third shear: x = 0 + (-0.41) * 0 = 0
   X= 0 | Y= 0
2. P(1;0):
   • First shear: x = 1 + 0,41 * 0 = 1
   • Second shear: y = 0 + 0.71 * 1 = 0.71
   • Third shear: x = 1 + (-0.41 * 0.71) = 0.708
   X= 0.708 | Y= 0.71
3. P(0;1):
   • First shear: x = 0 + (-0,41) * 1 = -0.41
   • Second shear: y = 1 + 0.71 * (-0.41) = 0.707
   • Third shear: x = -0.41 + (-0.41) * 0-707 = -0.71
   X= -0.71 | Y= 0.707
4. P(1;1):
   • First shear: x = 1 + (-0,41) * 0 = 0.59
   • Second shear: y = 1 + 0.71 * 0.59 = 1.41
   • Third shear: x = 0.59 + (-0.41) * 1.41 = 0.00
   X= 0.00 | Y= 1.41

To use this values in an program, it's necessary to "normalize" them, meaning to eliminate all negative values. This can be done by determining the minimum value of each axis and add it to all calculated values, This ensures, that the minimal value is 0.

Implementation

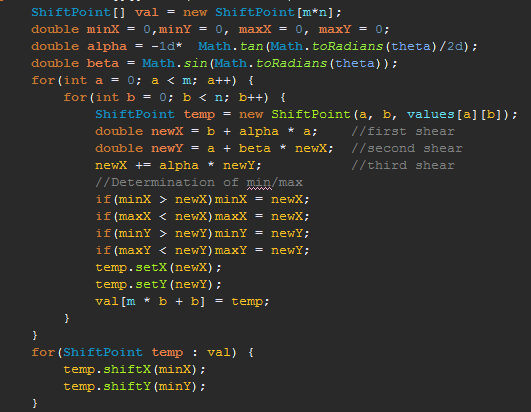
Here's an examplary implementation in Java:

Graphic representation of the rotation and normalization